Unlocking Electrical Circuits: The Art of Voltage Phasor Diagrams
Imagine trying to grasp the intricate dance of alternating currents, their voltages fluctuating like waves on a restless sea. How can we capture this dynamic interplay, these rhythmic oscillations of electrical energy? The answer lies in the elegant simplicity of the voltage phasor diagram, a visual language that transforms complex waveforms into static, easily interpretable vectors. This graphical representation allows us to see the relationship between voltage magnitudes and phase differences in alternating current (AC) circuits, offering a key to unlocking the secrets of electrical power.
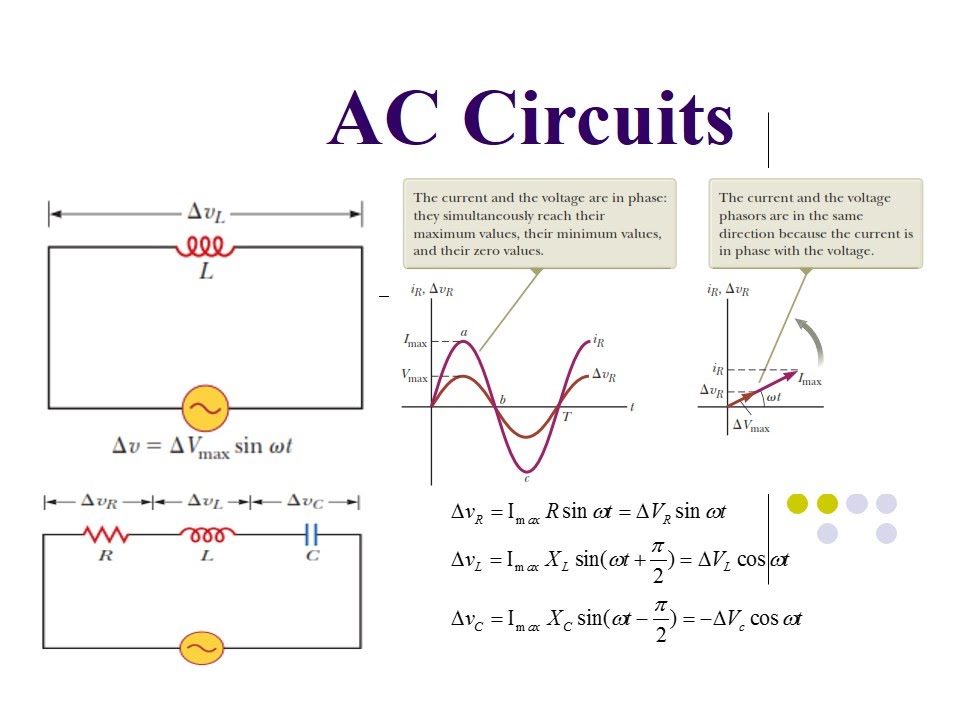
Visualizing the unseen forces at play within electrical circuits is a powerful tool for understanding their behavior. Phasor diagrams provide a window into this hidden world, representing sinusoidal voltages as rotating vectors. The length of the vector corresponds to the magnitude of the voltage, and its angle represents the phase shift relative to a reference. This approach simplifies the analysis of AC circuits, particularly those involving inductors and capacitors, where voltage and current are not necessarily in phase.
The concept of phasor diagrams emerged from the mathematical framework of complex numbers, offering a concise way to represent sinusoidal functions. Charles Proteus Steinmetz, a pioneering electrical engineer, played a crucial role in popularizing the use of phasors in AC circuit analysis in the late 19th century. Before the advent of phasor diagrams, analyzing AC circuits involving reactive components was a cumbersome process requiring complex trigonometric calculations. Phasor diagrams provide a more intuitive and efficient method, allowing engineers to easily visualize and analyze complex AC circuits.
Drawing a voltage phasor diagram is crucial for several reasons. It aids in understanding the phase relationships between voltages in different parts of a circuit. It simplifies the process of calculating resultant voltages in circuits with multiple AC sources. And, importantly, it helps in visualizing the impact of circuit elements like inductors and capacitors on the overall circuit behavior. Without phasor diagrams, understanding the dynamics of AC circuits would be a far more challenging endeavor.
At the heart of phasor diagrams lies the concept of representing sinusoidal quantities as rotating vectors. Imagine a vector rotating counter-clockwise at a constant angular velocity. The projection of this rotating vector onto a horizontal axis represents the instantaneous value of the sinusoidal voltage. The length of the vector corresponds to the peak voltage, and the angle it makes with the horizontal axis at any given moment represents the phase angle. This dynamic visualization captures the essence of alternating current and provides a foundation for understanding the significance of phasor diagrams.
One key benefit of sketching voltage phasor diagrams is the ability to visualize phase relationships. For instance, in a purely resistive circuit, the voltage and current are in phase, meaning their phasors align. However, in a circuit with an inductor, the voltage leads the current, depicted by the voltage phasor being ahead of the current phasor. This visual representation clarifies the phase difference and its implications for circuit behavior.
Another advantage is the simplification of calculations. By representing voltages as vectors, we can apply vector addition and subtraction to find the resultant voltage in circuits with multiple AC sources. This is significantly easier than manipulating trigonometric equations.
Finally, phasor diagrams provide insights into circuit design. By observing the relative positions and magnitudes of voltage phasors, engineers can understand the impact of different components on the overall circuit behavior. This understanding is crucial for optimizing circuit performance and troubleshooting potential issues.
Advantages and Disadvantages of Using Phasor Diagrams
| Advantages | Disadvantages |
|---|---|
| Simplifies AC circuit analysis | Only applicable to sinusoidal waveforms |
| Visualizes phase relationships | Can be complex for highly intricate circuits |
| Facilitates calculation of resultant voltages | Doesn't directly represent transient behavior |
Creating a voltage phasor diagram involves representing each AC voltage source as a rotating vector. The length of the vector represents the magnitude of the voltage, and the angle represents the phase shift relative to a reference. These vectors are then added vectorially to find the resultant voltage. A simple example would be a series circuit with a resistor and an inductor. The voltage across the resistor is in phase with the current, while the voltage across the inductor leads the current by 90 degrees. The phasor diagram would show two vectors, one representing the resistor voltage and the other representing the inductor voltage, with a 90-degree angle between them.
Best Practices:
1. Clearly label each phasor with its corresponding voltage.
2. Indicate the reference phasor.
3. Maintain consistent scaling for vector lengths.
4. Use a protractor for accurate angle measurement.
5. Choose a suitable reference frequency.
Frequently Asked Questions:
1. What is a phasor? A phasor is a rotating vector representing a sinusoidal quantity.
2. Why are phasor diagrams useful? They simplify AC circuit analysis and visualize phase relationships.
3. How do I determine the angle of a phasor? The angle represents the phase shift of the sinusoidal quantity.
4. Can phasor diagrams be used for non-sinusoidal waveforms? No, they are specific to sinusoidal waveforms.
5. What is the significance of the length of a phasor? The length represents the magnitude of the sinusoidal quantity.
6. How do I add phasors? Phasors are added vectorially, considering both magnitude and angle.
7. What is a reference phasor? A reference phasor is a chosen phasor against which other phasors are measured.
8. How can I learn more about phasor diagrams? Textbooks on circuit analysis and online resources offer detailed explanations.
In conclusion, mastering the art of sketching voltage phasor diagrams is essential for anyone seeking to understand the intricacies of AC circuits. From visualizing phase relationships to simplifying complex calculations, phasor diagrams provide a powerful tool for analyzing and designing electrical systems. Their ability to transform dynamic waveforms into static, interpretable vectors has revolutionized the way we approach AC circuit analysis. Embracing this graphical language opens doors to a deeper understanding of electrical power and its applications, enabling us to harness the full potential of alternating current. So, pick up your pencil, explore the world of phasors, and unlock the secrets of electrical circuits. The knowledge gained from understanding and applying phasor diagrams provides a crucial foundation for anyone working with AC circuits, from students to seasoned engineers. By visualizing the unseen dance of alternating currents, we gain the power to design, analyze, and innovate in the realm of electrical engineering. Start practicing today and empower yourself with this essential skill.
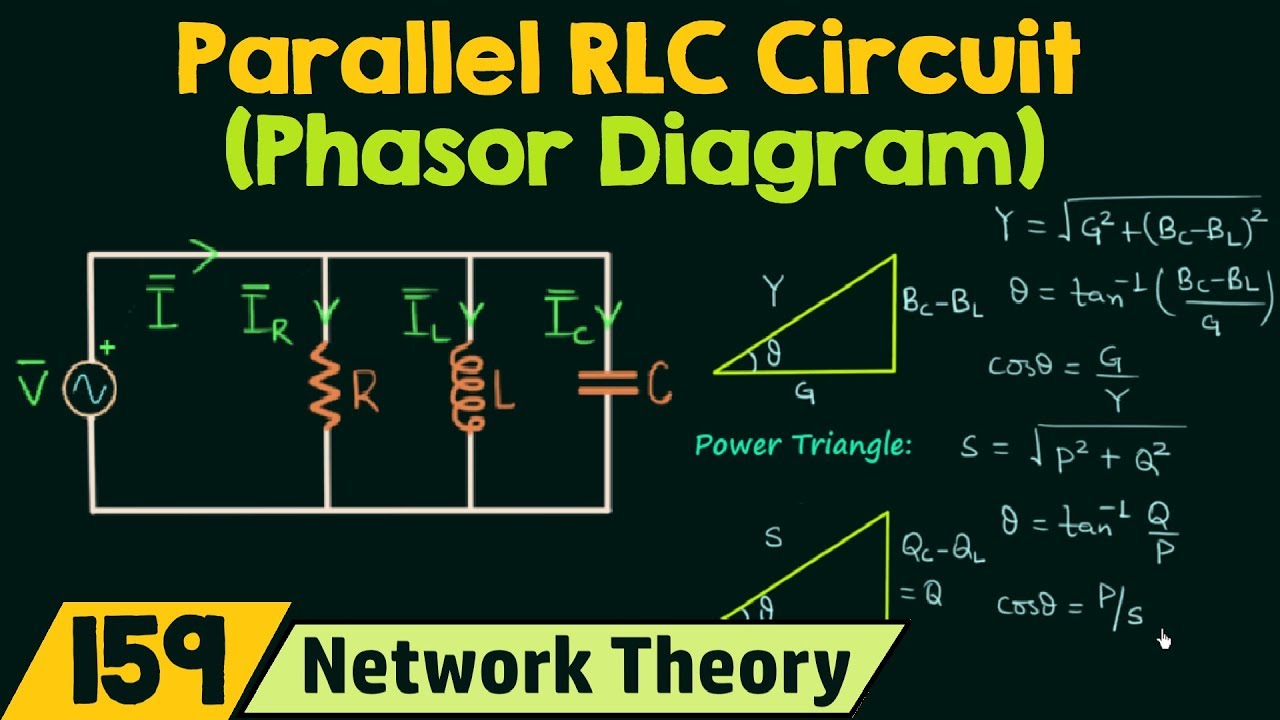
Series Parallel Rlc Circuit Phasor Diagram | YonathAn-Avis Hai
Solved Please draw the phasor diagram of a synchronous generator with | YonathAn-Avis Hai

How To Control Voltage In Power System at Daniel Richards blog | YonathAn-Avis Hai
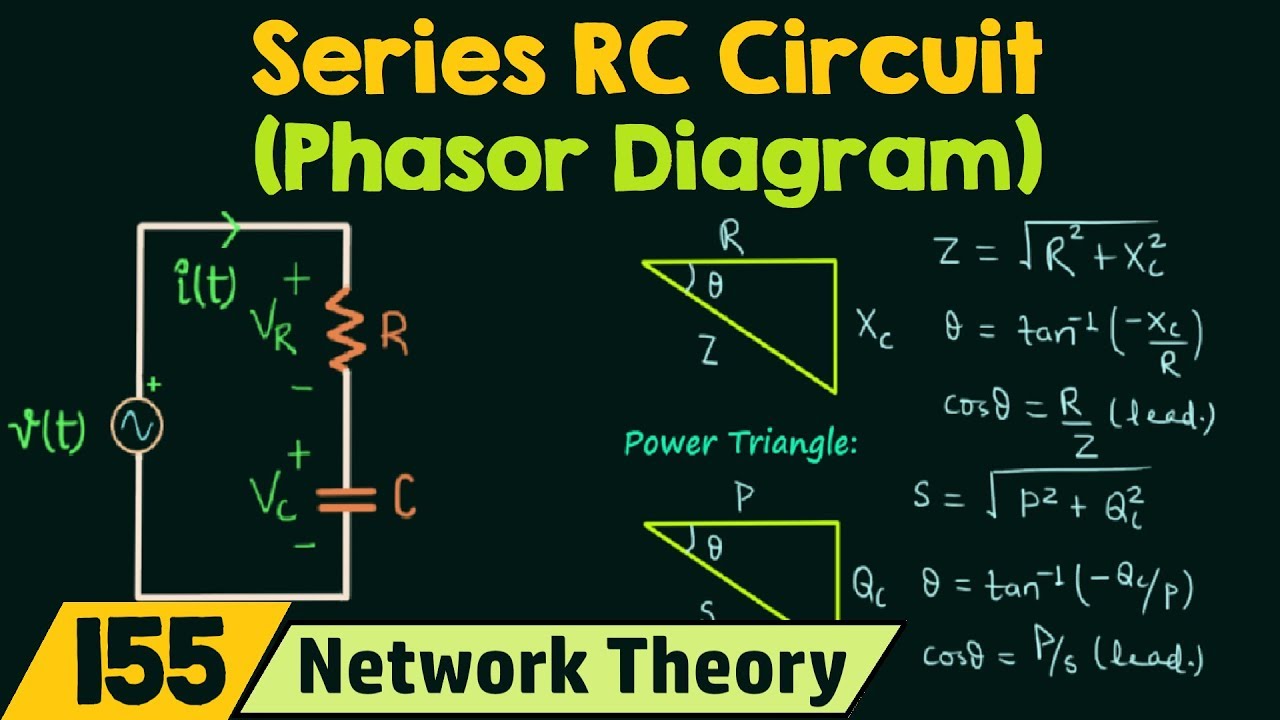
Rc Circuit Phasor Diagram | YonathAn-Avis Hai

DIAGRAM Single Phase Phasor Diagram | YonathAn-Avis Hai

Draw Phasor Diagram Rlc Circuit | YonathAn-Avis Hai

Phasor Diagram Of Rc Series Circuit | YonathAn-Avis Hai
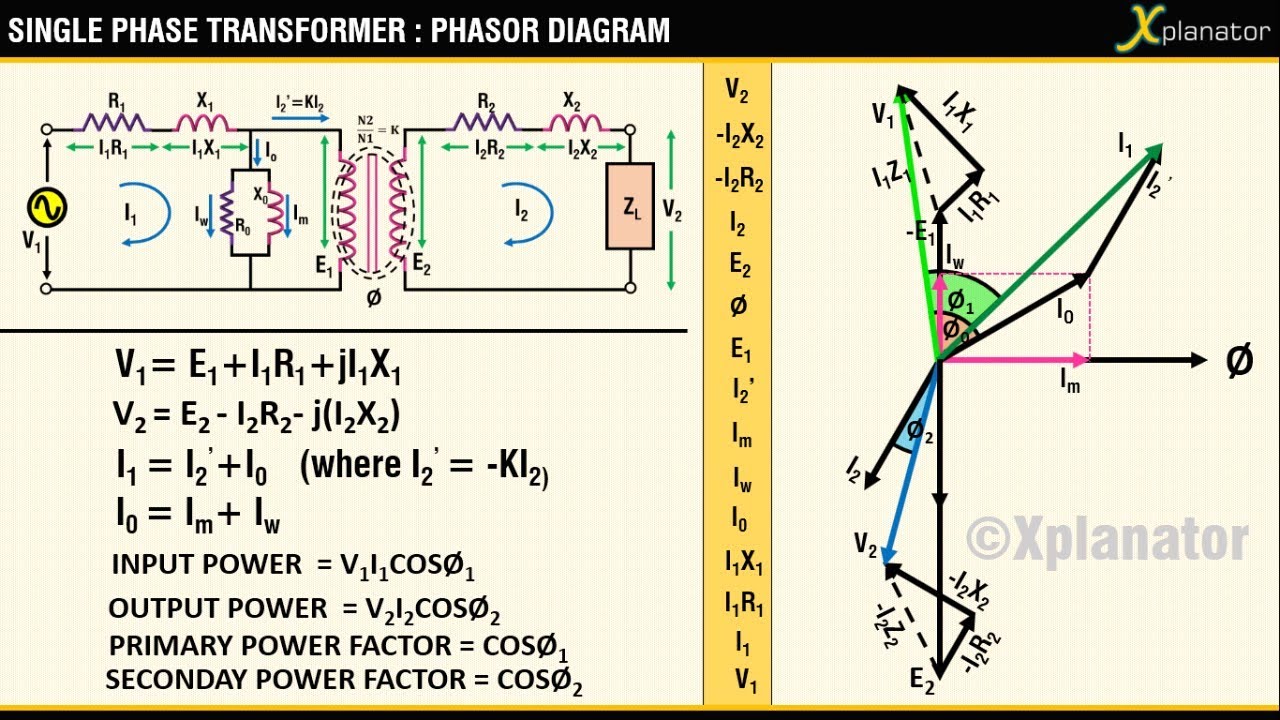
Inductive Circuit Phasor Diagram | YonathAn-Avis Hai

How To Draw A Phasor Diagram For 3 | YonathAn-Avis Hai
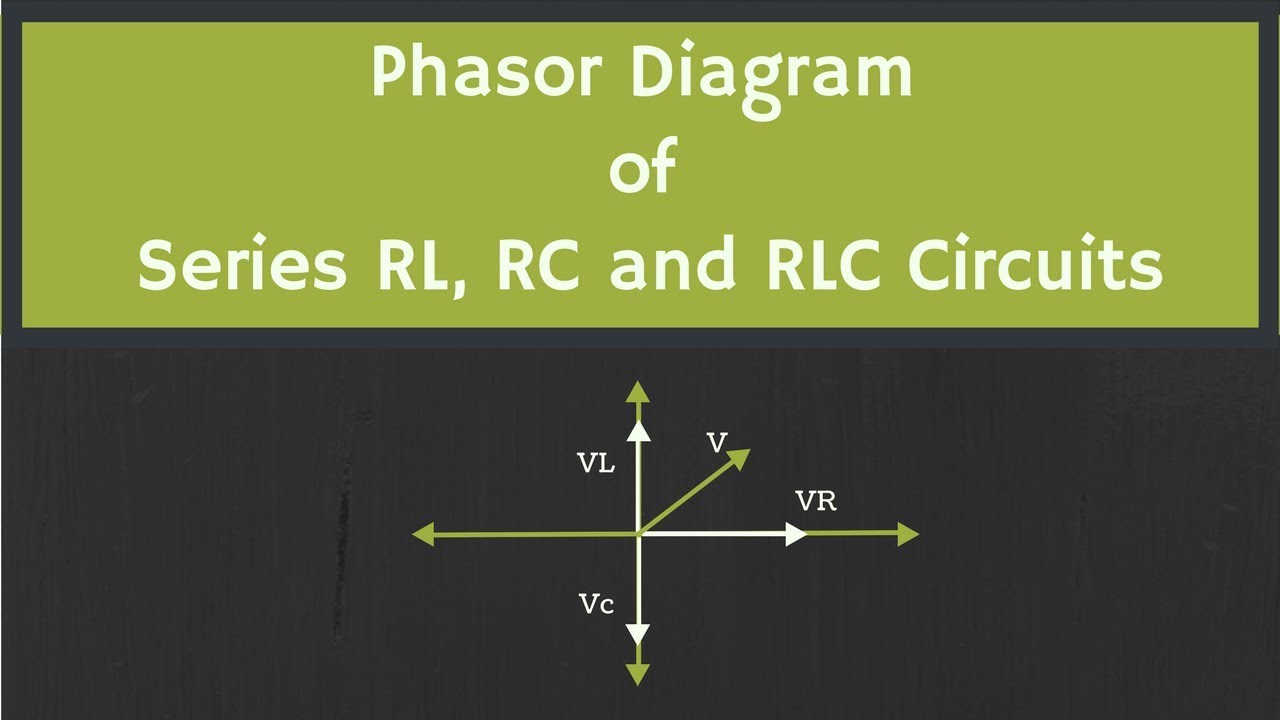
Phasor Diagram Rlc Circuit Series | YonathAn-Avis Hai

Basic Phasor Diagram Electric Circuit | YonathAn-Avis Hai
Phasor Diagram Of Capacitor In Ac Circuit | YonathAn-Avis Hai

How To Draw A Phasor Diagram | YonathAn-Avis Hai

How To Draw A Phasor Diagram Physics | YonathAn-Avis Hai

R L Circuit Phasor Diagram | YonathAn-Avis Hai