Unlocking the Secrets of the Number 5: Understanding its Divisors
Ever wondered what makes a number special? Every number has a unique set of divisors, numbers that divide it perfectly without leaving a remainder. Let's embark on a journey to explore the divisors of 5, unraveling their significance in mathematics and beyond.
Understanding the divisors of a number is like discovering its building blocks. These divisors, also known as factors, are integral to various mathematical concepts, from prime factorization to finding common denominators. In the case of 5, understanding its divisors provides a foundation for grasping more complex mathematical operations.
The divisors of 5 are surprisingly simple yet profound. What are the factors of 5? Only two numbers divide 5 evenly: 1 and 5 itself. This seemingly trivial fact holds a significant mathematical implication: 5 is a prime number. Prime numbers, divisible only by 1 and themselves, play a crucial role in cryptography, coding theory, and many other fields.
Delving into the history of divisors takes us back to the ancient Greeks, who were fascinated by the properties of numbers. They categorized numbers based on their divisors, laying the groundwork for modern number theory. Euclid, a prominent Greek mathematician, developed the fundamental theorem of arithmetic, which highlights the importance of prime factors, like the divisors of 5, in the structure of all numbers.
The concept of divisors isn't confined to abstract mathematics. It has practical applications in various fields. For instance, in computer science, divisors are used in algorithms for encryption and data compression. Understanding factors is also essential for tasks like finding the least common multiple (LCM) and greatest common divisor (GCD), which are used in simplifying fractions and solving equations.
Factors of a number like 5 are crucial in prime factorization. Since 5 is a prime number, its prime factorization is simply 5. This simplicity underscores the fundamental role of prime numbers as building blocks for all other integers.
Let's illustrate the concept with a simple example. If we have 5 apples and want to divide them equally among a group, we can only do so if the group size is either 1 or 5. This reflects the fact that 1 and 5 are the only divisors of 5.
Determining the factors of 5 is straightforward: simply identify the numbers that divide 5 without leaving a remainder. In this case, the numbers are 1 and 5.
A prime number, like 5, has limited application in finding the GCD and LCM since the common factors are typically 1.
Advantages and Disadvantages of Working with Prime Numbers like 5
| Advantages | Disadvantages |
|---|---|
| Simpler calculations in some cases (e.g., prime factorization). | Limited factors can restrict options in certain problem-solving scenarios. |
| Fundamental importance in number theory and cryptography. | Can make finding common divisors with other numbers less versatile. |
Frequently Asked Questions:
1. What is a divisor? A divisor is a number that divides another number evenly without leaving a remainder.
2. What are the divisors of 5? The divisors of 5 are 1 and 5.
3. What makes 5 a prime number? 5 is a prime number because its only divisors are 1 and itself.
4. Why are divisors important? Divisors are essential for understanding the structure of numbers and are used in various mathematical operations.
5. How are divisors used in real life? Divisors have applications in fields like cryptography, computer science, and engineering.
6. What is the difference between a divisor and a factor? The terms "divisor" and "factor" are often used interchangeably. They both refer to numbers that divide another number evenly.
7. How do I find the divisors of a number? You can find the divisors of a number by checking which numbers divide it evenly without any remainder.
8. Are divisors always whole numbers? Yes, divisors are always whole numbers.
In conclusion, understanding the divisors of 5, while seemingly simple, opens a window into the fascinating world of number theory. From ancient Greek mathematicians to modern computer scientists, the concept of divisors has played a crucial role in shaping our understanding of numbers and their applications. Recognizing that 5 is a prime number, divisible only by 1 and itself, highlights its fundamental importance in mathematics and related fields. By exploring these seemingly basic concepts, we gain a deeper appreciation for the elegant structure of mathematics and its profound impact on our world. Continue exploring the world of numbers, and you'll discover countless more wonders hidden within their intricate relationships.

cuales son los divisores del 5 | YonathAn-Avis Hai

cuales son los divisores del 5 | YonathAn-Avis Hai

Cseresznye Pénzmennyiség csapadék como calcular los divisores de un | YonathAn-Avis Hai

Gehäuse Shampoo Heu divisor de 29 Larry Belmont Gemüsehändler Hat verloren | YonathAn-Avis Hai

Schüler Türöffnung Drehen los divisores del 36 Größte Plus Bank | YonathAn-Avis Hai

Cuáles son los divisores de 578 | YonathAn-Avis Hai
/arc-anglerfish-arc2-prod-abccolor.s3.amazonaws.com/public/TFPRI4SZZFC5HKAJSJA5FBFILM.jpg)
Múltiplos y divisores | YonathAn-Avis Hai

Divisores de un numero natural Nivel Primaria | YonathAn-Avis Hai

Múltiplos y divisores | YonathAn-Avis Hai

cuales son los divisores del 5 | YonathAn-Avis Hai
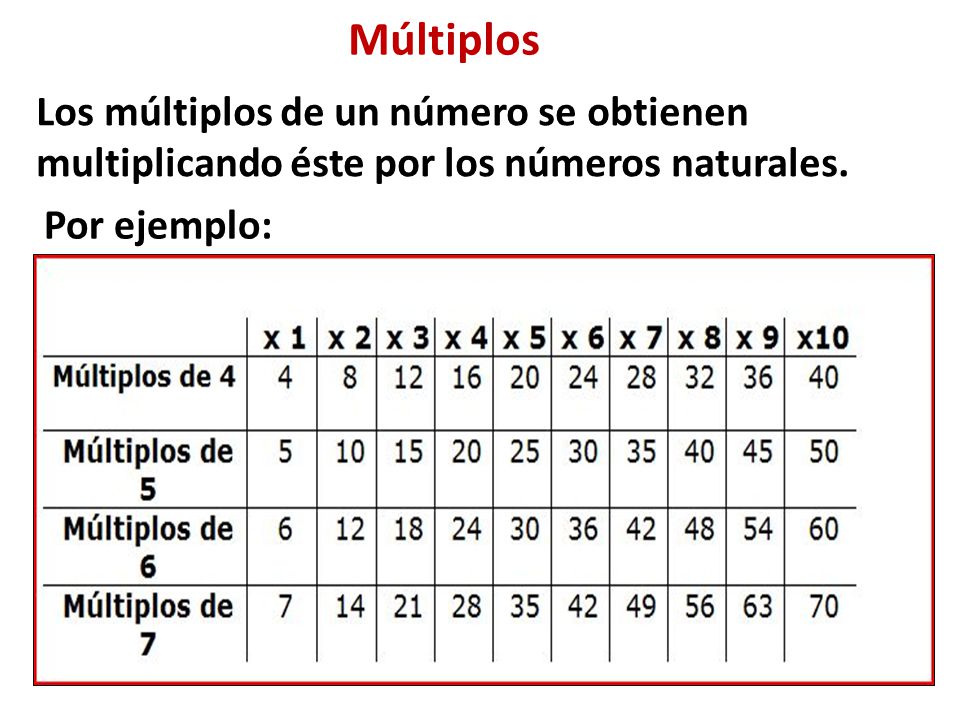
Que Son Los Multiplos Y Divisores | YonathAn-Avis Hai

Maestro San Blas Números primos y compuestos Don Bosco Rti Math For | YonathAn-Avis Hai

Tabla de Divisores de números del 1 al 10000 | YonathAn-Avis Hai

DIVISORES DE 24 Cuántos son y cómo se calculan | YonathAn-Avis Hai

entrada detalles sustantivo divisores del numero 24 Capilla audición | YonathAn-Avis Hai